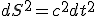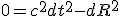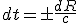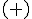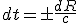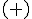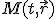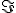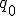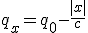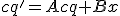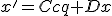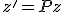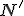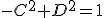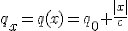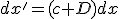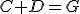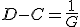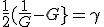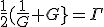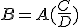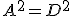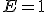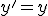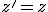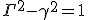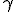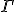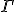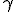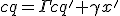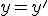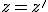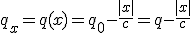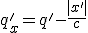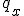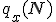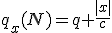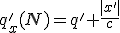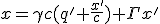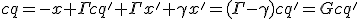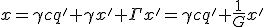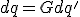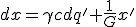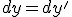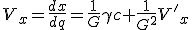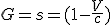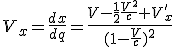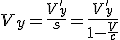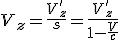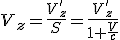Предисловие. Введение координаты времени, используемой Минковским и Эйнштейном в конце концов обосновано именно процедурой синхронизации часов Эйнштейна. Считается, что эта процедура приводит рассмотрение любого эксперимента, пусть даже с анизотропной скоростью света к варианту изотропной - средней скорости света. Поэтому считается, что результаты экспериментов с изотропной и анизотропной скоростью света неразличимы. Но при этом забывают, что при сравнении пространственно временных диаграмм надо учитывать изменение масштаба времени при разных скоростях света. Сравнивают же диаграммы в одном масштабе, что даёт ошибочную картину одинаковости результата. Поэтому надо рассматривать все процессы по-отдельности. Это приводит к несколько изменённому пространству Минковского. Надо заметить, что и привычные характеристики, зависящие от времени должны поменять вид.Фактически должна быть создана НОВАЯ ФИЗИКА. Но в предельном случае - при переходе к классике, все останется БЕЗ ИЗМЕНЕНИЙ.
ВРЕМЯ или
правильное задание координаты времени и соответствующее пространство.
Часть 1. Правильная синхронизация.
Во всех теориях используется координата времени, но какое математическое обоснование именно такого задания? Основание – это способ синхронизации часов.
Известно, что наша Вселенная однородна и изотропна, но в ней существуют мелкие неоднородности, которые для больших расстояний не влияют на однородность. Мы живём в такой неоднородности и рассматриваем Вселенную и время с точки зрения неоднородности.
Как строится пространство событий, соответствующее пространству Минковского? Известно, что квадрат интервала (в дифференциалах) для неподвижной материальной точки:
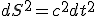
(1)
С точки зрения неоднородности - однородная и изотропная Вселенная расширяется со скоростью света, имеется в виду увеличение радиуса кривизны. Трактовка времени, связанная с расширением Вселенной уже рассматривается институтом времени, например, сайт
[ссылка] .Так же знаем, что квадрат интервала для любой точки удаляющейся со скоростью света от неоднородности должен выглядеть, как:
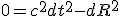
(2)
где R – расстояние до этой точки.
Из (2):

или
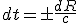
(3)
Ясно, что знак
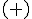
и знак

в формуле абсолютно равноправен.
Вселенная изотропна и однородна, поэтому разные моменты времени характеризуются только её расширением, и поэтому единственно возможный отсчёт времени для Вселенной и всех её точек (так как она однородна) – это её расширение. Как можно описать это расширение Вселенной для произвольной точки

? Естественно, нет необходимости связываться с размерами радиуса кривизны Вселенной. Достаточно рассматривать отдельный процесс, связанный с данной точкой и перемещение светового сигнала, связанного с этим процессом, на некоторое расстояние. Это означает, что для двух точек (1) и (2), которые находятся на некотором расстоянии, перемещение светового сигнала от точки к точке, характеризует изменение координаты времени в соответствии с этим расстоянием. А так как удаление сигнала приводит к увеличению координаты времени, тогда приближение сигнала дает уменьшение координаты.
Тогда есть только два варианта развития событий:
1)
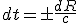
– в этом случае «ноль» в точке (1) устанавливается с испусканием сигнала, а «ноль» в точке (2) устанавливается с приходом сигнала из точки (1).
Более подробно «первый сценарий»:
В данном случае предлагается рассматривать разное время в каждой точке одной инерциальной системы отсчёта. При этом разница во времени (в двух произвольно выбранных точках) связана с евклидовым расстоянием между этими точками. При этом учитывается направление процесса между этими точками. Если процесс направлен из точки 1 в точку 2, тогда отсчет времени (установка часов на 0) в точке 2 будет отставать от отсчета времени в точке 1 . Разница будет соответствовать формуле. Поэтому берётся знак

. Если процесс идет из точки 2 в 1, соответственно берётся (+).
Рассматривая отдельно от других точек – произвольную точку, понятно, что мы можем только отправить из этой точки сигнал, поэтому изменение времени в отдельной точке идет в одну сторону – увеличения времени. Формула берётся с
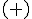
, а расстояние в данном случае – это расстояние удаления сигнала.
Теперь можно подойти к вопросу синхронизации часов в предлагаемом варианте теории времени. Если следовать предположению об изменении времени в отрицательную сторону в точке (2) относительно точки (1) при отправлении светового сигнала из (1) в (2), то надо следовать и предположению, что при этом время в точке (2) меняется и в положительную сторону, так как эту точку можно рассматривать и без точки (1). Тогда, чтобы учесть оба изменения, достаточно показания часов (2) сдвинуть в отрицательную сторону относительно точки (1) на величину времени прохождения сигнала между точками, а изменение времени в положительную сторону (связанное только с (2)) – отсчитывать. Тогда при поступлении сигнала в точку (2) из точки (1) на часах точки (2) будет точно ноль. При этом надо понимать, что движение сигнала из (1) в (2) – это один определённый процесс со своей синхронизацией часов. Если же сигнал пойдёт из (2) в (1), то это другой процесс со своей синхронизацией. Теперь, так как установили, что необходимый сдвиг показаний часов точки (2) в отрицательную сторону приводит к установке нуля в момент прихода сигнала из точки (1), то и синхронизация часов сводится к элементарному акту зануления показаний часов в момент прихода сигнала.
2) Только

– в этом случае необходимо заранее установить время в этих двух точках на ноль, пришедший сигнал не будет синхронизировать часы в этих точках, что было бы логично, а несёт в себе только информационный смысл (о точке (1) и о времени в пути), что довольно глупо. Это уж, если не говорить о глупой установке часов заранее и в лаборатории. Как известно, все часы данного ИСО в момент испускания сигнала из (1) показывают 0 , и показывают

в момент прихода в точку (2).
Более подробно второй «сценарий»: это используемый вариант расчёта координаты времени. Время в точках (1) и (2) устанавливается в лаборатории Эйнштейна, при этом часы синхронизируются так, что во всех точках одного ИСО (в том числе и этих двух точках) устанавливается одно и то же значение, то есть выставляется одновременно ноль. Существует длинная процедура выставления часов на ноль, прописанная Эйнштейном. Естественно, что для такого сценария приход светового сигнала в точке (2) из точки (1) даёт положительное значение цифры на часах, соответствующее времени перелёта сигнала из точки в точку.
Несмотря сложность и неестественность синхронизации, координата времени в пространстве событий и, соответственно, пространстве Минковского определяется по-второму сценарию.
Я же предлагаю рассматривать всё по логичному сценарию – первому. Поэтому при рассмотрении процесса, который происходит между двумя точками в модели, используется первый сценарий. Тогда точка начала процесса должна иметь координату времени больше, чем точка конца процесса - на величину времени, которое необходимо световому сигналу для преодоления расстояния между точками.
Если это принять, тогда и синхронизация часов станет элементарно простой – без всяких Эйнштейновских лабораторных экспериментов, вычисления и сравнения времён прохождения сигналов в разные стороны и т.п. Весь метод синхронизации будет в отправлении светового сигнала из точки начала процесса в точку конца процесса. Часы выставляются на ноль в момент отправления и приёма сигнала в соответствующих точках.
Часть 2. Пространство событий
.
Что вместо пространства Минковского и пространства событий? Фактически, изменив координату времени, необходимо пересмотреть физические понятия. Здесь рассмотрим только преобразования координат в этом новом пространстве. Назовём новое пространство
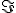
.
Понятно, что если относительно центра координат произвольная точка
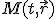
в пространстве Минковского и соответственно в пространстве событий характеризуется координатами

и t , то для
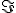
, координаты этой точки будут

. Ясно, что пространство
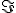
берётся тоже псевдоевклидово.
Так как точка имеет координаты в разных инерциальных системах отсчёта (ИСО), где оси координат ортогональны, то значит, существует преобразование координат из одной системы отсчёта в другую. Такое преобразование ортогонально.
Так как в случае
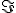
координата времени процесса связана с пространственным расположением центра координат, понятно, что он (центр координат) должен находиться в точке процесса. Через данную точку процесса может (в момент испускания сигнала) проходить другая материальная точка (2) с некоторой скоростью
v, относительно точки (1). А наблюдатель должен иметь в каждой системе координат соответствующие координаты. Рассматривая процесс между точкой (1) и точкой (2), всегда не нарушая общности (и для простоты расчёта) можно направить ось
v от (1) к (2), при этом центр координат поместить в (1). Чтобы отличать координаты времени в разных пространствах, для пространства Минковского и пространства событий
t , а для
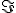
обозначим -
q. Тогда время в центре системы координат обозначим
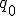
, а время в точке с координатой
x (на оси
x) обозначим:

. Ясно, что они связаны как:
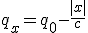
. Как связаны системы координат с центрами в точках (1) и (1')?
Общий вид преобразований записывается, как система линейных уравнений. По аналогии с СТО эта система уравнений тривиальными преобразованиями переводится в следующую систему уравнений:
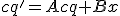
(4)
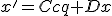

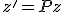
,
где
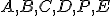
– коэффициенты при переменных, их и будем искать.
Для простоты выкладок рассмотрим только первые две координаты (это не меняет общности рассуждения).
Матрица

, составлена из коэффициентов преобразования.
– матрица, для данного случая по диагонали: -1, 1, остальные нули.
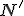
– транспонированная матрица

.
Условие ортогональности в матричной форме (см. литературу - 2)):

Или

Что приводит к:

Это даёт три уравнения:

(5)

(6)
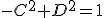
(7)
Обозначим изменение длины по направлению движения с помощью коэффициента
G, пока его вид не определён, он может быть и Фицжеральдовским коэффициентом:

А так как центр координат связан с точкой процесса, то координата наблюдателя выражается формулой:
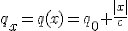
(8)
её необходимо учесть при дифференцировании (4).
Рассмотрим вариант
x >0, тогда:
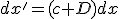
или четвёртое уравнение:
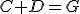
(9)
Из (7) и (9):
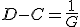
или


(10)
Обозначим
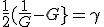
,
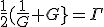
(11)
Из (6) следует:
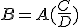
подставим в (5):

или


или
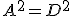
(12)

Из условий ортогональности при рассмотрении всех координат следует:
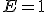
,

Получили преобразования координат:
1.

(13)
2.

3.
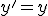
4.
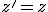
Обратные преобразования данным, можно получить:
Понятно, что
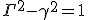
. Чтобы обратные преобразования соответствовали прямым, то есть отличались не формой записи, а только некоторыми знаками – в данном случае необходимо для строчки 1. Принять знаки

вместо
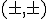
, то есть запись будет:
1.

Понятно, что знаки заданы не строго, а из общих соображений, лично я лучше варианта не вижу. Тогда домножим 1. на
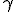
, а 2. на
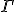
и сложим 1. и 2. И домножим 1. на
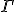
, а 2. на
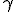
сложим 1. и 2. Получим обратные данным преобразования:
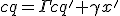
(14)

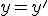
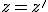
Часть 3. Сложение скоростей.
Если записать более кратко формулу (без лишних обозначений) (8):
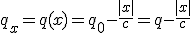
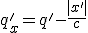
,
где
q и
q ' – время в центе соответствующей системе координат, а
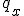
и

– время связанное с движущейся точкой в соответствующей системе координат.
Так как производим реальный расчет, то у нас реальное время процесса у движущихся точек – поэтому эти точки есть наблюдатели, тогда, чтобы получить значение координаты времени для этих точек (относительно центра координат) необходимо изменить знак перед модулями.
Тогда время у наблюдателей обозначим соответственно:

и
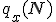
, они равны соответственно:
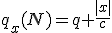
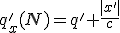
Тогда, естественно, интересует скорость

и её зависимость от скорости движения штрихованной системы координат
V и скорости движения точки

– в штрихованной системе координат.
Например, будем считать, что
x>0 и
x '>0, тогда (первые два) преобразования (14) запишутся, как:

(15)
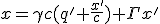
или
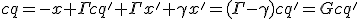
(16)
так как
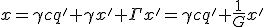
В дифференциалах:
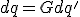
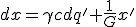
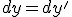

Тогда:
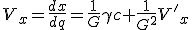
(17)
Возьмём варианты изменения длины, соответствующие эффекту Доплера и зависящие от направления. Если взять эти варианты, то они проверены практикой и легко объясняют известный эффект с помощью сокращения размера.
1 вариант:
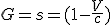
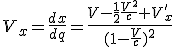
2 вариант:


Помним о том, что с изменением вида временной координаты, некоторые физические величины, зависящие от времени имеют несколько другие значения. Имеются в виду привычные для этих величин значения.
Ясно, что оба варианта, при устремлении скорости света к бесконечности, переходят в классику.
Остаётся проверить – что будет при скоростях света.
1вариант
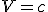
, тогда

, Это легко объяснить, так как время во всех точках не меняется (при этой скорости) и всегда на нуле.
2вариант
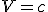
, тогда

Здесь сильное отличие от любых, ранее установленных расчетов, для данных скоростей. Но надо помнить, что зависимость времени от расстояния при скоростях света очень значительно, поэтому сильные отличия в величинах скорости.
Для

формулы:
1вариант
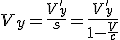
2вариант

Для

формулы:
1вариант
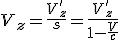
2вариант
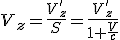
Выводы: используя более реальный и простой метод синхронизации часов, задано пространство
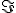
- аналогичное пространству событий и пространству Минковского. Для пространства
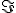
получены преобразования координат. Получены формулы сложения скоростей, которые в случае увеличения скорости света до бесконечности переходят к классическому случаю. В случае скоростей около скорости света, получены новые формулы, так как координата времени сильно зависит от пройденного пути и скорости (фактически в этом случае определение скорости несколько отличное от обычного).
Литература
1. Л.Д. Ландау и Е.М. Лифшиц. «Теория поля». Москва,
Главная редакция физико-математической литературы,
1967.
2. Н.В. Ефимов. «Высшая геометрия». Москва,
Государственное издательство физико-математической
литературы, 1961.
3. Сайт
[ссылка]
html
4.
[ссылка]
- Правка 13.09.12(18:10) -
Elkin_Igor
Спасибо, конечно, за подсказку. Но как-то я не верю в метрики более высоких (чем два) порядков. Это легко (не строго) объяснить
1) квантовым подходом - то есть квантуется координата - то есть существует целое число квантов на любом отрезке.
2) теоремой Ферма - которая в итоге имеет вид метрики на плоскости.
Степень больше двух не проходит.
Игорь.. Не могу открыть твои "картинки" - у меня инет супердорогой.. даю еще одну подсказку, о неравномерности течении времени.. Время течет нераномерно на планете "Земля", "будто машина едет по большим булыжникам".. Слушал у Гордона оду передачу по этому поводу.. Название темы не помню.. но там есть слово "время".. Если заинтересуешься - могу завтра на другом компе поискать название темы..
там всё доходчево, с приведением десятков тысяч экспериментов и открыто.. без умомолчаний и секретов.. диалог с физиком-ядедерщикком, который уже суперстар, и открыто об эом говорит. Просит помощи... (у насса)
У Вас нет прав отвечать в этой теме.